
一、相遇问题
【意义】
两个物体从两地出发,相向而行,经过一段时间,必然会在途中相遇,这类题型就把它称为相遇问题。
【区别】
相遇问题是研究速度,时间和路程三者数量之间关系的问题。它和一般的行程问题区别在:不是一个物体的运动,所以,它研究的速度包含两个物体的速度,也就是速度和。
【相遇问题的关系式】
速度和×相遇时间=路程
路程÷速度和=相遇时间
路程÷相遇时间=速度和
【解题思路和方法】
简单的题目可直接利用公式,复杂的题目变通后再利用公式。
【基本题型】
1、甲、乙两辆汽车从相距680km的两地同时相对开出,甲车每小时行驶80km,乙车每时行驶90km,几时后两车在途中相遇?
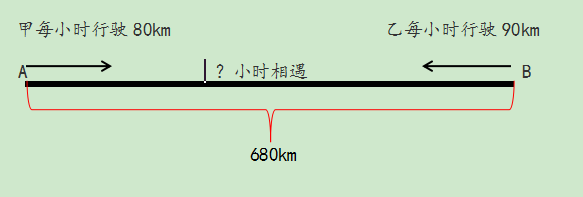
算术方法:直接运用公式,路程÷速度和=相遇时间
680÷(80+90)
=680÷170
=4(时)
答:4时后两车在途中相遇。
用方程解: 根据速度和×相遇时间=路程等量关系列方程
解设:X时后两车在途中相遇。
(80+90)× X=680
170 X=680
X=680÷170
X=4
答:4时后两车在途中相遇。
【变形类相遇题型】
1、甲、乙两车从相距895km的两地相对开出,甲车每时行驶110km,乙车每时行驶95km。几时后两车还差75km才能相遇?
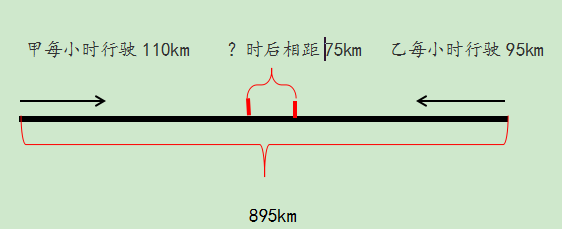
解题思路:本题两车还差75km才能相遇,这个75km两车没有行走,所以两车共行的路程变化了,也就是895-75=820km。然后套用公式就可以了。
算术方法:
(895-75)÷(110+95)
=820÷205
=4(时)
答:4时后两车还差75km就能相遇。
用方程解:
方法一:
等量关系:两车已行的+两车未行的=总路程
解:设x时后两车还差75km就能相遇。
(110+95)×x+75=895
205X+75 =895
205X=820
X=4
答:4时后两车还差75km就能相遇。
方法二:
等量关系:速度和×相遇时间=总路程-两车未行的路程
解:设x时后两车还差75km就能相遇。
(110+95)×x=895-75
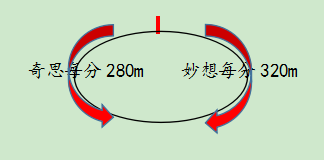
2、奇思每分跑280m,妙想每分跑320m。环湖公路一周的长度是5400m,两人同时反方向跑步,多长时间后两人再次相遇?
解题思路:两人再次相遇,说明跑了全程的二周,也就是路程的2倍,共行的路程是5400×2=10800m
算术方法:5400×2÷(280+320)
用方程解:
等量关系式:速度和×相遇时间=路程×2
解:设x分后两人再次相遇。
(280+320)×x=5400×2

【试一试】
1、甲乙两人同时从两地骑车相向而行,甲车平均每小时20KM,乙车的平均速度每小时18KM,两人相遇时距离中点3KM,全程长多少千米?
2、A、B两地相距5100M,甲、乙两人同时从两地相向而行。甲每分钟行90M,乙每分钟行80M。如果有一只狗与甲同行,狗每分钟跑150M,当狗遇到乙时立即返回,遇到甲后又向乙跑去。这样,狗不停地在甲、乙之间往返跑,直到两人相遇为止。那么狗跑的路程是多少米?
3、甲乙两个工程队合修一条长200km的公路。甲队每天修5km,乙队每天修7km,两队同时从两头开始施工,多少天他们还相距20km?
4、AB两地相距278千米,甲车从A地开往B地,每小时行76千米,半小时后,乙车从B地开往A地,每小时行84千米,乙车开出几小时后和甲车相遇?

